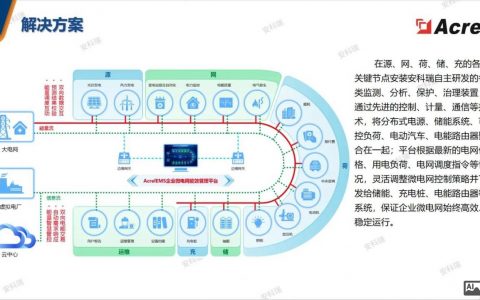
在Stata中,漏斗图(Funnel Plot)是用于评估多篇研究结果一致性或发表偏倚的常用可视化工具,尤其适用于Meta分析,漏斗图的横轴通常为效应量(如OR值、RR值、SMD值等),纵轴为标准误或样本量的倒数,通过散点的对称性判断是否存在发表偏倚——若散点呈对称的倒漏斗形,提示无明显偏倚;若不对称,则可能存在发表偏倚(如阴性结果未发表),以下是Stata实现漏斗图的详细步骤及命令解析,涵盖数据准备、基础绘图、高级调整及结果解读。

数据准备与效应量计算
漏斗图绘制前需先计算效应量及其标准误,以Meta分析为例,常用命令为metan,需预先整理数据为“研究ID-事件数-总样本量”或“效应量-标准误”格式,纳入5项研究的二分类数据(事件数、总样本量),数据格式如下:
| study | events1 | n1 | events2 | n2 |
|---|---|---|---|---|
| 1 | 30 | 100 | 20 | 100 |
| 2 | 25 | 120 | 18 | 120 |
| 3 | 15 | 80 | 10 | 80 |
| 4 | 40 | 150 | 35 | 150 |
| 5 | 20 | 90 | 15 | 90 |
使用metan计算OR值及其标准误:
metan events1 n1 events2 n2, or label(namevar=study) eform
上述命令中,or指定计算OR值(比值比),eform以指数形式显示结果(如OR值及其95%CI),label(namevar=study)将研究ID作为散点标签,执行后,metan会自动生成效应量(ES)和标准误(SE)的变量,默认命名为_ES和_SE,后续绘图可直接调用。
基础漏斗图绘制
Stata中绘制漏斗图的核心命令为meta funnel,需基于metan输出的效应量和标准误变量,基础命令如下:
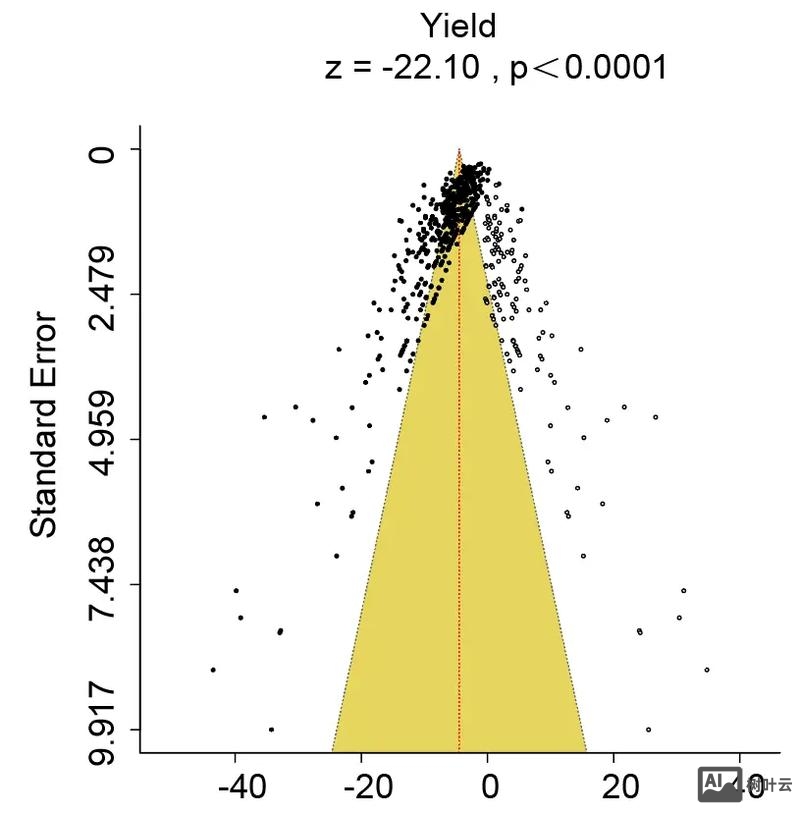
meta funnel _ES _SE
该命令会生成以_ES(效应量)为横轴、_SE(标准误)为纵轴的漏斗图,默认添加垂直参考线(效应量=0)和95%置信区间边界线(帮助判断对称性)。
关键选项说明
studyvar():指定研究标识变量(如studyvar(study)),使散点显示研究名称,便于识别异常研究。ci():添加效应量的置信区间(如ci(95)),需提前通过meta esize等命令计算CI变量。square:将散点替换为方形,避免重叠点遮挡(适用于研究数量较多时)。 )和xtitle()ytitle()自定义图表标题和坐标轴标签,如title(“漏斗图:OR值发表偏倚评估”) xtitle(“Log(OR)”) ytitle(“SE(Log(OR))”)`。
高级调整与美化
转换坐标轴(常用对数/反正弦变换)
当效应量为OR或RR等非对称分布指标时,横轴通常采用对数尺度(Log尺度)以增强对称性,通过log选项实现:
meta funnel _ES _SE, log title("Log(OR)漏斗图")若为连续变量(如SMD),可使用asinh(反正弦双曲函数)变换:
meta funnel _ES _SE, asinh
添加趋势线与置信区间
通过fit()选项添加回归趋势线,辅助判断发表偏倚(如Egger检验的线性回归线):
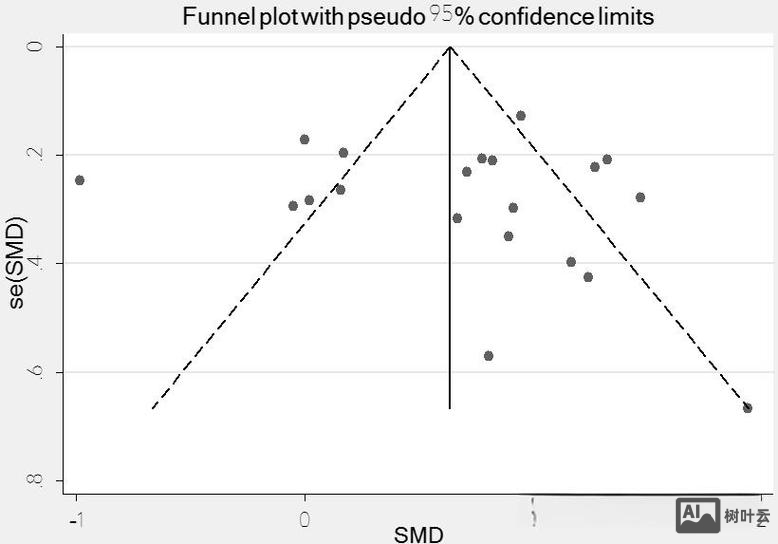
meta funnel _ES _SE, fit(lincom) // 添加线性回归线
fit()支持多种模型,如fit(rigls)(随机效应模型趋势线)。
调整散点样式与颜色
使用msymbol()(散点符号)、mcolor()(颜色)和size()(大小)美化图形:
meta funnel _ES _SE, msymbol(O) mcolor(blue%50) size(medium) title("美化后漏斗图")%50表示颜色透明度(50%),避免重叠点完全遮挡。
导出高清图片
通过graph export命令导出为PDF/SVG格式(矢量图,适合期刊投稿):
graph export "funnel_plot.pdf", replace width(3000) height(2400)
结果解读与发表偏倚判断
漏斗图的核心是观察散点分布的对称性:
- 对称分布:散点均匀分布于垂直参考线两侧,呈倒漏斗形,提示无明显发表偏倚(如右侧图1)。
- 不对称分布:散点偏向右侧(效应量较大侧),提示可能存在发表偏倚(阴性结果或小样本阴性研究未发表),或异质性过大(如右侧图2)。
若发现不对称,可结合Egger检验(meta bias命令)或Begg检验进一步验证:
meta bias _ES _SE, egger
常见问题与解决方案
散点重叠严重,难以识别单个研究?
解决:使用jitter()选项为散点添加随机抖动,或改用square/triangle等符号:
meta funnel _ES _SE, jitter(5) msymbol(square) // jitter(5)控制抖动强度
如何添加伪95%置信区间边界线?
解决:通过meta summarize计算平均标准误,手动绘制边界线(以SE为纵轴,边界线SE=1.96/√n):
meta summarize _ES _SE local se_upper = 1.96 / sqrt(r(mean_n)) // 假设平均样本量为r(mean_n) twoway (scatter _ES _SE) (function y=`se_upper', range(min max) lpattern(dash)), // 添加上边界线
相关问答FAQs
Q1:漏斗图中纵轴为什么有时用标准误(SE),有时用样本量倒数(1/n)?
A1:纵轴选择取决于效应量类型和统计假设,标准误(SE)直接反映效应量的估计精度,适用于多数Meta分析;而样本量倒数(1/n)是SE的近似(当事件率接近50%时,SE≈√[p(1-p)/n]≈1/(2√n)),更直观展示“大样本效应更精确”的原理,但需注意仅适用于二分类变量且p≈0.5的场景,Stata的meta funnel默认以SE为纵轴,若需1/n,可手动生成gen n_inv=1/n后替换纵轴变量。
Q2:漏斗图不对称时,除了发表偏倚,还有哪些可能原因?
A2:漏斗图不对称不完全是发表偏倚,其他常见原因包括:①异质性:研究间存在临床或方法学异质性(如人群特征、干预措施差异),导致效应量分布偏移;②方法学质量差异:低质量研究(如随机化不严格)可能高估效应量,造成不对称;③真实效应量的非线性关系:如剂量反应研究中,效应量与样本量存在非线性关联;④机会:研究数量较少时(如<10项),随机误差可能导致假性不对称,此时需结合森林图、敏感性分析(如剔除低质量研究)和异质性检验(如I²统计量)综合判断。
文章来源网络,作者:运维,如若转载,请注明出处:https://shuyeidc.com/wp/410326.html<